TRIBUN-BALI.COM, DENPASAR – Mari kita belajar bersama! Inilah kunci jawaban Matematika kelas 10 Kurikulum Merdeka halaman 116 117 118, kegiatan siswa Latihan 4.1.

Kali ini akan membahas soal pada bab ke 3 yang berjudul Perbandingan Trigonometri pada kegiatan siswa Latihan 4.1 tentang menghitung pengukuran pertama ke dalam persamaan matematika.

Kunci jawaban di bawah ini diharapkan bisa membantu siswa sebagai alternatif jawaban untuk menyelesaikan soal pada halaman 116 117 118 di buku siswa Matematika kelas 10.

Berikut kunci jawaban dan pembahasan soal Matematika Kelas 10 Kurikulum Merdeka halaman 116 117 118 sesuai dengan buku Matematika kelas 10 edisi tahun 2023.

Baca juga: Kunci Jawaban Matematika Kelas 10 Kurikulum Merdeka Halaman 111 112 113, Eksplorasi 4.1: Bola

(Update Kunci Jawaban)

Kunci Jawaban Matematika Kelas 10 Halaman 116 117 118 Kurikulum Merdeka

Latihan 4.1

1. Asep memiliki beberapa jenis tongkat untuk olahraga: tongkat kasti, tongkat hoki, dan tongkat bisbol.

Asep menjajarkan 3 tongkat kasti, 2 tongkat hoki, dan 1 tongkat bisbol dan panjangnya 455 cm.

Asep menjajarkan sebuah tongkat kasti, 3 tongkat ukuran hoki, dan 2 tongkat bisbol dan panjangnya 545 cm.

Asep juga mengamati bahwa 2 tongkat kasti sama panjang dengan tongkat bisbol.

Jawaban:

Jika k : panjang tongkat kasti, h : panjang tongkat hoki, dan b : panjang tongkat bisbol.

Baca juga: Kunci Jawaban Matematika Kelas 10 Kurikulum Merdeka Halaman 103 104, Uji Kompetensi Bab 3

a. Tuliskan pengukuran pertama ke dalam persamaan matematika.

Jawaban:

3k + 2h + b = 455

3k + 2h + 2b = 545

2k - b = 0

b. Tuliskan hasil pengukuran kedua dan ketiga ke dalam persamaan matematika juga untuk menghasilkan sistem persamaan.

Jawaban:

3k + 2h + b = 455 (x3) => 9k + 6h + 3b = 1365

k + 3h + 2b = 545 (x2) => 2k + 6h + 4b = 1090 (-)

= 7k - b = 275

c. Apakah sistem persamaan itu sebuah sistem persamaan linear? Bagaimana kamu tahu?

Jawaban:

Ya, sebuah sistem persamaan linear, karena semua variabelnya berpangkat satu.

Baca juga: Kunci Jawaban Matematika Kelas 10 Kurikulum Merdeka Halaman 99 100 101, Latihan 3.7: Trigonometri

d. Selesaikan sistem persamaan tersebut.

Jawaban:

7k - b = 275

2k - b = 0 (-)

5k = 275

k = 55

e. Ada berapa solusi yang ada?

Jawaban:

Ada satu solusi, yaitu k = 55 , h = 90 , dan b = 110 .

f. Berapakah panjang tiap jenis tongkat?

Jawaban:

Tongkat kasti panjangnya 55 cm, tongkat hoki panjangnya 90 cm, dan tongkat bisbol panjangnya 110 cm.

2. Sebuah minuman dijual dalam tiga kemasan berbeda: kecil, sedang, dan besar.

Jika Bonar membeli 3 kemasan kecil, 2 kemasan sedang, dan 3 kemasan besar, dia mendapat minuman sebanyak 4.700 ml.

Jika Bonar membeli 3 kemasan kecil, 1 kemasan sedang, dan 2 kemasan besar, dia mendapat 3.300 ml.

Jika Bonar membeli 2 kemasan sedang dan 2 kemasan besar, dia mendapat 2.800 ml minuman. Berapakah volume tiap jenis kemasan?

a. Tuliskan sistem persamaan yang bersesuaian dengan permasalahan tersebut.

Jawaban:

Sistem persamaannya

3k + 2s + 3b = 4700

3k + s + 2b = 3300

2s + 2b = 2800

b. Apakah sistem persamaan itu termasuk sistem persamaan linear? Tuliskan alasannya.

Jawaban:

Semua variabel pada sistem persamaan tersebut berpangkat satu, maka sistem persamaan tersebut adalah sistem persamaan linear.

c. Selesaikan sistem persamaan tersebut.

Jawaban:

Eliminasi persamaan pertama dan persamaan kedua.

3k + 2s + 3b = 4700

3k + s +2b = 3300 (-)

s + b = 1400

Persamaan yang dihasilkan adalah persamaan yang sama dengan persamaan ketiga dalam sistem persamaan linear (seluruh persamaan dikalikan 2).

d. Ada berapa solusi yang ada? Jelaskan.

Jawaban:

Proses pada (c) menghasilkan persamaan yang sama dengan persamaan ketiga (grafiknya berupa dua garis berimpit), maka sistem persamaan linear ini memiliki banyak solusi.

e. Apa artinya bagi Bonar jika sistem persamaan linear ini memiliki banyak solusi?

Jawaban:

Ada banyak kemungkinan volume kemasan kecil, sedang, dan besar, contohnya adalah solusi, k = 333,333, s = 500, b = 900 juga solusi

3. Bu Wati membeli tiga jenis buah. Kalau ia membeli 3 kg jeruk, 3 kg pepaya, dan 1 kg salak, ia harus membayar Rp130.000,00.

Jika Bu Wati membeli 2 kg jeruk, 2 kg pepaya, dan 1 kg salak, ia harus membayar Rp100.000,00. Jika Bu Wati mau membeli 1 kg jeruk dan 1 kg pepaya, ia harus membayar Rp50.000,00.

Berapakah harga tiap kg setiap jenis buah?

a. Tuliskan sistem persamaan yang bersesuaian dengan permasalahan tersebut.

Jawaban:

Jika j adalah harga tiap kg jeruk, p adalah harga tiap kg pepaya, dan s adalah harga tiap kg salak (semua harga dalam ribu rupiah), maka sistem persamaannya adalah:

3j + 3p + s = 130

2j + 2p + s = 100

j + p = 50

b. Apakah sistem persamaan itu termasuk sistem persamaan linear? Tuliskan alasannya.

Jawaban:

Sistem persamaan linear karena semua variabelnya berpangkat satu.

c. Selesaikan sistem persamaan tersebut.

Jawaban:

Eliminasi persamaan pertama dan kedua diperoleh:

3j + 3p + s = 130

2j + 2p + s = 100 (-)

j + p = 30

Bandingkan persamaan ini dengan persamaan ketiga.

d. Ada berapa solusi yang ada? Jelaskan.

Jawaban:

Grafiknya berupa dua garis yang sejajar, maka sistem persamaan linear ini adalah sistem persamaan linear yang tidak memiliki solusi.

e. Apa artinya bagi Bu Wati jika sistem persamaan linear ini tidak memiliki solusi?

Jawaban:

Harga buah-buahan di setiap paket berbeda-beda.

4. Untuk setiap model matematika berikut, tentukan apakah model matematika tersebut merupakan sistem persamaan linear atau bukan.  Jelaskan.

Ayo, Berpikir Kritis

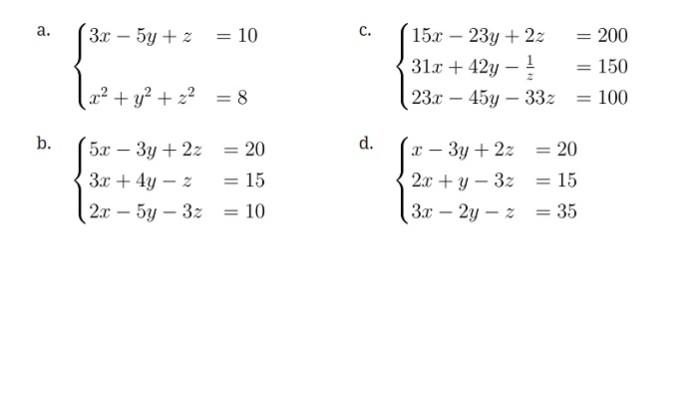
Jawaban:

a. Bukan sistem persamaan linear, ada variabel x"2 Bukan sistem persamaan linear, ada variabel x"2, x"2, z"2

b. Sistem persamaan linear, semua variabel berpangkat 1.

c. Bukan sistem persamaan linear, ada variabel 1/2

d. Sistem persamaan linear, semua variabel berpangkat 1.

5. Pak Musa memiliki toko beras dan menjual campuran beras. Campuran 2 kg beras A, 2 kg beras B, dan 1 kg beras C dihargai Rp50.000,00.

Campuran 4 kg beras A, 2 kg beras B, dan 3 kg beras C dihargai Rp91.000,00.

Campuran 4 kg beras A, 4 kg beras B, dan 2 kg beras C dihargai Rp95.000,00.

Tentukan harga tiap kg beras A, beras B, dan beras C.

a. Tuliskan model matematikanya.

Jawaban:

Jika a adalah harga 1 kg beras A, b harga 1 kg beras B, dan c adalah harga 1 kg beras C, maka

2a + 2b + c = 50

4a + 2b + 3c = 91

4a + 4b + 2c = 95

b. Apakah model matematika itu merupakan sistem persamaan linear?

Jawaban:

Sistem persamaan linear karena semua variabelnya berpangkat satu.

c. Ada berapa solusi yang dimiliki oleh sistem ini? Bagaimana kamu tahu?

Jawaban:

2a + 2b + c = 50 (x2) => 4a + 4b + 2c = 100

4a + 4b + 3c = 95 (x1) => 4a + 4b + +2c = 95 (-)

Perhatikan bahwa ruas kiri kedua persamaan sama sedangkan ruas kanannya berbeda. Ini adalah ciri sistem persamaan linear yang tidak memiliki solusi.

Keterangan: (") berarti pangkat, (/) berarti per atau se per, (√) akar dari, (*) berarti derajat

Demikian kunci jawaban Matematika kelas 10 Kurikulum Merdeka halaman 116 117 118, Latihan 4.1 sesuai dengan buku siswa Matematika edisi tahun 2023.

Disclaimer

Kunci jawaban diatas bersifat alternatif jawaban sehingga para siswa bisa memberikan eksplorasi jawaban lain.

Kunci jawaban soal diatas bisa saja berbeda sesuai dengan pemahaman tenaga pengajar atau murid. (*)