TRIBUNNEWS.COM - Olimpiade Sains Nasional (OSN) 2026 akan segera digelar. Saat ini, rangkaian kegiatan OSN telah memasuki tahap pendaftaran peserta yang dibuka hingga Sabtu, 28 Februari 2026.

OSN merupakan ajang kompetisi akademik berskala nasional yang diselenggarakan oleh pemerintah dengan tujuan menjaring, membina, serta mengembangkan potensi dan bakat peserta didik jenjang SD, SMP, hingga SMA/SMK di bidang sains dari seluruh Indonesia.

Pelaksanaan OSN dilakukan melalui empat tahap seleksi, yaitu seleksi tingkat sekolah (OSN-S), tingkat kabupaten/kota (OSN-K), tingkat provinsi (OSN-P), dan tingkat nasional yang terdiri atas babak semifinal dan final.

Untuk jenjang SD dan SMP, mata pelajaran yang diperlombakan meliputi Matematika, Ilmu Pengetahuan Alam (IPA), dan Ilmu Pengetahuan Sosial (IPS). Sementara itu, pada jenjang SMA/SMK, bidang lomba lebih beragam, mencakup Matematika, IPA, IPS, Fisika, Kimia, Biologi, Informatika, Astronomi, serta Ekonomi.

Mengutip laman resmi Kemendikdasmen, berikut disajikan contoh soal OSN Matematika SMP tingkat kabupaten/kota yang dapat digunakan sebagai bahan latihan bagi para peserta.

Soal OSN Matematika SMP Tingkat Kabupaten/Kota

1. Misalkan N (a, b, c) menyatakan banyaknya kelipatan a yang lebih besar dari b dan kurang dari c. Sebagai contoh, N (3, 5, 10) = 2 karena terdapat dua bilangan antara 5 dan 10 yang merupakan kelipatan 3. Nilai dari N (6³, 6⁴, 6⁶) adalah ....

A. 216
B. 215
C. 209
D. 208

Kunci Jawaban: D

2. Gina bermain angka dengan mengisikan bilangan bulat 1, 2, ..., 9 pada tabel 3 × 3. Sehingga, hasil kali ketiga bilangan pada setiap baris adalah bilangan yang terdapat di kanan tabel dan hasil kali ketiga bilangan pada setiap kolom adalah bilangan yang terdapat di bawah tabel, seperti terlihat sebagai berikut.

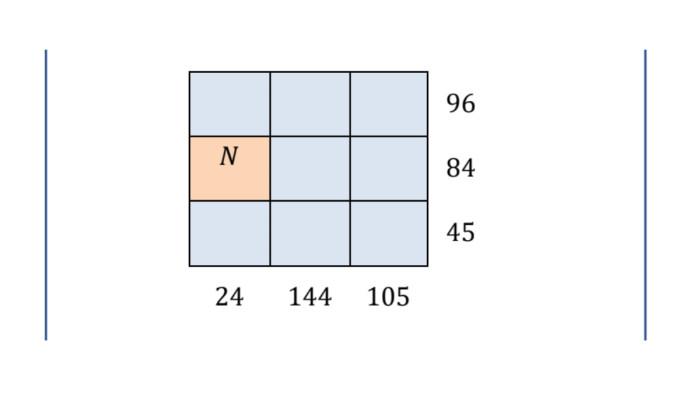
Nilai N adalah ....

A. 1
B. 3
C. 4
D. 6

Kunci Jawaban: D

Baca juga: 50 Soal OSN IPS SMP 2026 dan Kunci Jawaban Olimpiade Sains Nasional

3. Bilangan-bilangan 4, 5, 6, 9, 11, 12, 18, 20, dan 24 akan diletakkan pada 4 lingkaran dan 5 persegi yang disusun dalam satu baris sebagai berikut.

Setiap bilangan harus digunakan tepat satu kali dan diletakkan di tempat yang berbeda. Selain itu, bilangan pada setiap lingkaran harus merupakan hasil penjumlahan dari dua bilangan pada persegi yang berada tepat di sebelah kiri dan kanannya. Jika x adalah bilangan pada persegi paling kiri dan y adalah bilangan pada persegi paling kanan, maka nilai terbesar yang mungkin dari x + y adalah ....

A. 32
B. 38
C. 42
D. 44

Kunci Jawaban: A

4. Banyaknya faktor dari 2024 yang lebih besar dari √2024 adalah ....

A. 4
B. 8
C. 12
D. 16

Kunci Jawaban: B

5. Diketahui x merupakan bilangan bulat positif kelipatan 2 yang kurang dari 50, y merupakan bilangan bulat positif kelipatan 3, dan y − x = 10. Jika A adalah himpunan semua faktor prima dari x, B adalah himpunan semua faktor prima dari y, dan jumlah semua anggota dari A ∪ B adalah 10, maka nilai dari x + y adalah ....

A. 14
B. 26
C. 38
D. 50

Kunci Jawaban: C

6. Suatu bilangan bulat positif n disebut bilangan JUMPAT jika jumlah n bilangan bulat positif pertama dapat dinyatakan sebagai penjumlahan empat bilangan bulat positif berurutan. Banyaknya bilangan JUMPAT yang kurang dari 2024 adalah ....

A. 252
B. 253
C. 504
D. 505

Kunci Jawaban: D

7. Diketahui A = {0, 1, 2, ... , 9} dan rstu adalah bilangan empat digit dengan r, s, t, u adalah anggota A yang berbeda.
Jika rstu + stu = vwxyz , dengan r, s, t, u, v, w, x, y, z adalah anggota A yang berbeda, maka anggota A yang tidak digunakan dalam operasi penjumlahan tersebut adalah ....

A. 2
B. 3
C. 5
D. 8

Kunci Jawaban: B

8. Jika bilangan real positif p, q, r, s memenuhi sistem persamaan p² + q² = r² + s² , p² + s² − ps = q² + r² + qr, nilai dari pq + rs / ps + qr adalah .... 

A. √23 
B. √22 
C. √33 
D. √32

Kunci Jawaban: A

9. Diketahui pertidaksamaan √x − 3 + √6 − x ≥ p memiliki penyelesaian untuk x ∈ R. Nilai p terbesar yang mungkin adalah ...

A. √6
B. 3
C. √6 + √3
D. 6

Kunci Jawaban: B

10. Diketahui a, b, dan c adalah bilangan ratusan yang satuannya sama dengan ratusannya. Jika b = 2a + 1 dan c = 2b + 1, maka banyaknya kemungkinan tripel (a, b, c) yang berbeda adalah ....

A. 1
B. 2
C. 3
D. 4

Kunci Jawaban: B

11. Jika x³ + 1/x³ = 18 dan x ≠ 0, maka nilai dari x⁷ + 1/x7 + 7 adalah ....

A. 845
B. 850
C. 855
D. 860

Kunci Jawaban: C

12. Diketahui persamaan x⁴ + ax³ + 54x² − 108x + 81 = 0 dengan a bilangan real, memiliki 4 akar real berbeda, yaitu r1, r2, r3, r4. 

Jika r1 × r2 × r3 × r4 = (r1 + r2 + r3 + r4)/4 )⁴

maka nilai dari a adalah ....

A. −12
B. −8
C. 3
D. 12

Kunci Jawaban: A

13. Diketahui sistem persamaan sebagai berikut dengan a, b, dan c adalah bilangan real positif.

• a = bc
• b = c(a + 2)
• c = b(a − 2)

Nilai dari a² + b² + c² adalah ....

A. 15
B. 15 − 4√5
C. 225
D. 15 + 4√5

Kunci Jawaban: D

14. Suatu segi delapan ABCDEFGH dibentuk dari suatu persegi ABCD dan persegi panjang EFGH yang panjang sisi-sisinya merupakan bilangan bulat positif. Contoh segi delapan tersebut diberikan pada gambar berikut.

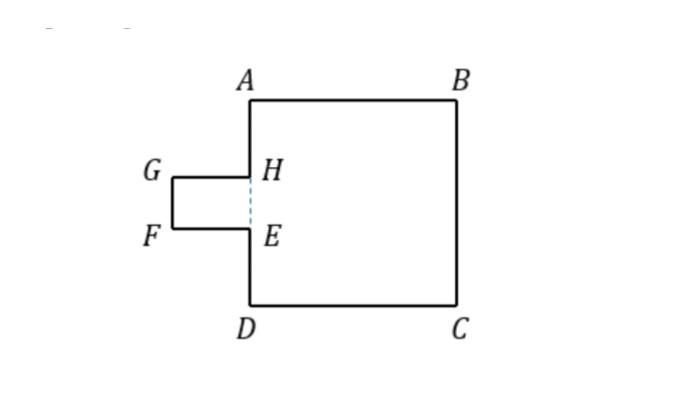
Jika luas persegi adalah x cm², luas persegi panjang adalah y cm², x > y, dan xy =  8, maka keliling segi delapan ABCDEFGH yang mungkin adalah ... cm.

A. 30
B. 33
C. 34
D. 51

Kunci Jawaban: C

15. Diketahui segitiga sama kaki ABC dengan AB = BC = 8 cm dan ∠ABC = 120°. Titik tengah AB dan BC masing-masing adalah D dan E. Garis DF tegak lurus AB dan EF tegak lurus BC. Luas daerah yang diarsir adalah ... cm².

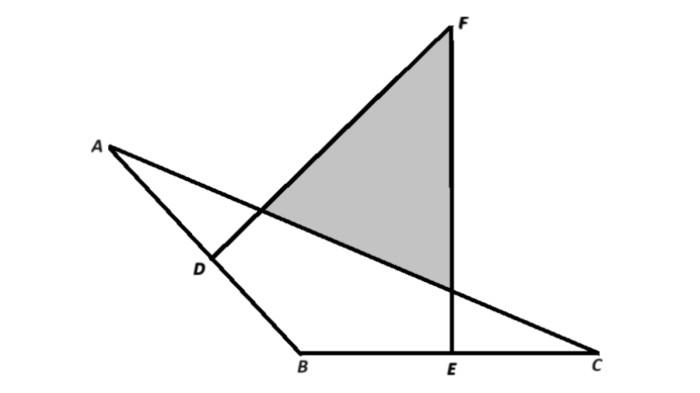
A. 8/3 √3
B. 16/3 √3
C. 8√3
D. 16√3

Kunci Jawaban: A

16. Perhatikan gambar berikut.

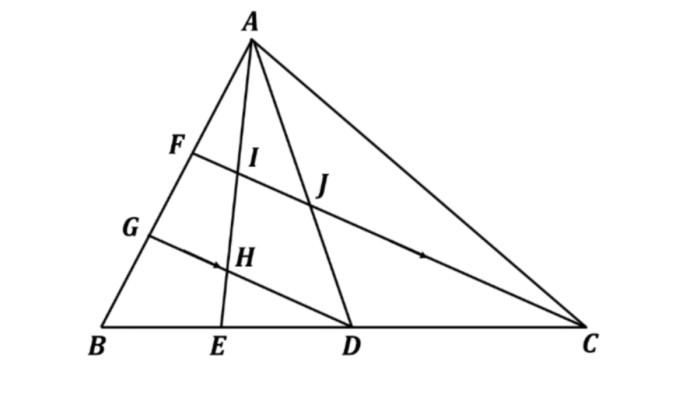
Diketahui panjang BD = CD, BE = DE, AJ = JD dan DG sejajar CF. Jika perbandingan luas daerah segitiga ADH dan segitiga ABC dinyatakan dalam bentuk paling sederhana m: n, maka nilai dari m + n adalah ....

A. 5
B. 6
C. 7
D. 8

Kunci Jawaban: C

17. Segi enam beraturan ABCDEF memiliki panjang sisi 2024 mm. Titik G adalah titik tengah AB dan titik H adalah titik tengah EG. Perbandingan luas daerah segitiga CDH dan segi enam ABCDEF adalah ....

A. 4:24
B. 5:24
C. 6:24
D. 7:24

Kunci Jawaban: C

18. Diberikan 4 bola pejal berukuran sama dengan diameter 22 cm dan sebuah silinder dengan diameter 46 cm. Dua bola diletakkan di dasar silinder dengan jarak pusat keduanya 24 cm. Dua bola sisanya juga dimasukkan ke dalam silinder dengan jarak antar pusat keduanya 24 cm dan garis yang menghubungkan kedua pusat bola ini tegak lurus dengan garis yang menghubungkan kedua pusat bola sebelumnya.
Jika air dimasukkan ke dalam silinder hingga menutupi seluruh permukaan bola, maka volume minimum air yang dimasukkan adalah .... cm³.

A. 307 1/3 π
B. 529 1/3 π
C. 1694π
D. 7098 2/3 π

Kunci Jawaban: B

19. Diketahui suatu kerucut dengan titik puncak T, pusat sisi alas O, dan diameter alas AB. Titik C berada pada ruas garis AT dengan AC = OC = 11 cm. Titik D merupakan titik potong antara garis OT dan BC dengan DC = 7 cm. Volume kerucut tersebut adalah ... cm³.

A. 196π
B. 960π
C. 1960π
D. 9600π

Kunci Jawaban: C

20. Sekelompok bilangan berbeda terdiri dari 6 bilangan genap dan 4 bilangan ganjil. Dari kelompok bilangan tersebut diperoleh informasi sebagai berikut.

• Jangkauan data = 24.
• Jangkauan antar kuartil = 14.
• Bilangan ke-3, 5, 6 dan 8 adalah bilangan ganjil.
• Median = 2024.
• Rata-rata bilangan ganjil adalah 2022.

Rata-rata terbesar yang mungkin dimiliki oleh kelompok bilangan tersebut adalah ....

A. 2022
B. 2022,4
C. 2024
D. 2024,4

Kunci Jawaban: D

21. Empat bilangan asli kurang dari sepuluh memiliki rata-rata, median dan modus tunggal yang membentuk tiga bilangan asli berurutan.
Jika A adalah jumlah terkecil yang mungkin dari empat bilangan tersebut dan B adalah jumlah terbesar yang mungkin dari empat bilangan tersebut, maka nilai dari A + B adalah ....

A. 36
B. 40
C. 42
D. 44

Kunci Jawaban: C

22. Dari segi lima ABCDE dipilih 21 titik yang berbeda. Satu titik dari sisi AB, dua titik dari sisi BC, tiga titik dari sisi CD, empat titik dari sisi DE, lima titik sudut A, B, C, D, E, dan enam titik dari sisi AE. Banyaknya segitiga yang dapat dibentuk dari seluruh titik yang dipilih adalah ....

A. 560
B. 770
C. 1239
D. 1330

Kunci Jawaban: D

23. Jumlah semua bilangan ratusan yang ketiga digitnya berbeda dan tidak memuat 0 adalah ....

A. 359.640
B. 279.720
C. 277.200
D. 252.000

Kunci Jawaban: B

24. Sepuluh persegi panjang kecil dengan ukuran 1 cm × 2 cm akan digunakan untuk membentuk persegi panjang besar dengan ukuran 10 cm × 2 cm. Banyaknya cara membentuk persegi panjang besar terebut adalah ....

Keterangan: Berikut adalah beberapa contoh cara membentuk persegi panjang besar yang mungkin untuk dilakukan.

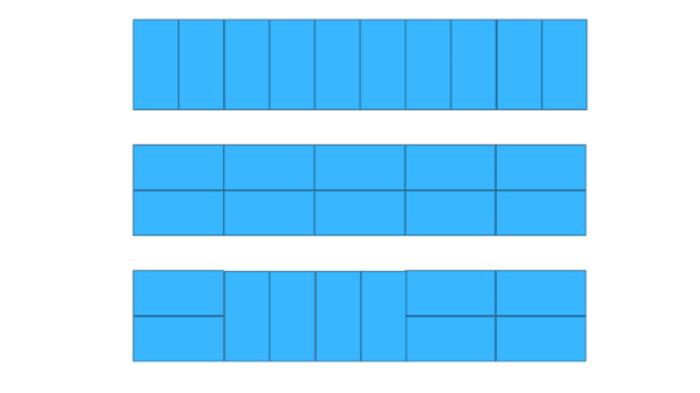
A. 78
B. 89
C. 144
D. 233

Kunci Jawaban: B

25. Atlet bulu tangkis Anthony Ginting menjalani pertandingan persahabatan dengan Jonathan Christie, rekan sesama timnya. Pertandingan berakhir jika salah satu pemain menang dua set langsung atau menang dua set dari tiga set permainan (rubber set). Tim pelatih Ginting menyatakan bahwa peluang Ginting dapat memenangkan suatu set adalah 1,6 kali lipat peluang Ginting memenangkan pertandingan. Misalkan tidak ada pertandingan yang berakhir imbang/seri. Berdasarkan pernyataan tim pelatih Ginting, peluang Jonathan memenangkan pertandingan adalah ....

A. 1/4
B. 3/4
C. 5/32
D. 27/32

Kunci Jawaban: A

26. Diketahui A dan B bilangan dua digit, C bilangan tiga digit, dan A + B = C. Tujuh digit bilangan A, B, C tersebut, yaitu 1, 2, 4, 5, 6, 7, 8 yang masing-masing digunakan tepat satu kali. Digit satuan  dari C adalah 6. Bilangan C yang dimaksud adalah….

A. 176
B. 186
C. 246
D. 256

Kunci jawaban: B

27. Di rumah pak budi yang sedang di tinggal pergi berlibur lampu teras di beri saklar otomatis yang akan mulai menyala pada pukul 19.00 atau 19.30 atau 20.00 atau 21.00 secara acak. lampu tersebut kemudian akan otomatis padam pada suatu titik waktu anatar pukul 04.00 sampai pukul 06.00 pagi harinya. misalkan diketahui pada malam ini lampu tersebut menyala selamat t jam, peluang bahwa lampu menyala selama 9

A. 1/12
B. 1/8
C. 1/6
D. 1/4

Kunci jawaban: C

28. Di babak bonus suatu kuis, seorang peserta akan di minta untuk mengambil secara acak 5 dari 20 bola yang telah di nomori 1 sampai 20 hadiah utama akan di dapatkan jika selisih nomor setiap pasang bola tidak kurang dari 3. banyaknya kemungkinan peserta tersebut memenangkan hadiah utama adalah.....

A. 816
B. 1008
C. 1140
D. 1260

Kunci jawaban: B

29. Sandi memiliki 12 kandang hamster yang terdiri dari 3 kandang warna hijau 3 warna merah, 3 warna biru dan 3 warna kuning terdapat 10 ekor hamser yang akan di distribusikan ke dalam kandang-kandang tersebut. ia mendistribusikan 4 hamster ke dalam kandang warna hijau selanjutnya mendistribusikan 3 hamster ke dalam kadang warna merah, 2 hamster ke dalam kadang warna biru, serta seekor hamster ke dalam kandang warna kuning asumsikan masing masing hamster memiliki kemungkinan yang sama untuk di masukan ke dalam kadang tertentu. Tentukan peluang bahwa kadang hijau berisi lebih banyak hamster di banding kandang lain baik kandang  hijau yang sewarna maupun kadang lain warna.

A. 1/9
B. 2/9
C. 1/3
D. 4/9

Kunci jawaban: B

30. Diberikan himpunan A = {1,2,3, ..., 25}. Banyak himpunan bagian berunsur dua yang hasil kali unsur-unsurnya kuadrat sempurna adalah ....

A. 40
B. 45
C. 50
D. 55

Kunci jawaban: D

A. 35/4096
B. 21/4096
C. 35/2048
D. 21/2048​

Kunci jawaban: A

32. Diketahui bilangan x dan y, masing-masing tidak lebih dari 2018 dan x² + y² habis dibagi 121. Jika pasangan (x,y) dan (y,x) tidak dibedakan, maka banyak pasangan (x,y) yang memenuhi adalah ....

A. 168
B. 170
C. 173
D. 176

Kunci jawaban: C

33. Suatu tabung berada di dalam prisma tegak segitiga. Tabung tersebut tepat menyinggung prisma pada alas, tutup, dan semua sisi prisma. Alas prisma berbentuk segitiga sama sisi dengan panjang sisi 8 cm dan tinggi prisma 6 cm Volume tabung tersebut adalah ....

A. 48π
B. 64π
C. 96π
D. 144π

Kunci jawaban: B

34. Misalkan suku-suku suatu barisan diberikan dengan x1 = 1, x_n+1 = xn + n, untuk n > 1. Nilai n terbesar sehingga x₁ + x₂ + x₃ + ... + x_n ≤ 2018 adalah ....

A. 18
B. 19
C. 20
D. 21

Kunci jawaban: C

35. Diketahui x dan y adalah dua bilangan bulat positif, banyak (x,y) sehingga kelipatan pengurangan terkecil dari x dan y sama dengan 2³,3³,5³ adalah….

A. 9
B. 18
C. 27
D. 36

Kunci jawaban: C

36. Jika A = [ a, b, c] dengan a, b dan c merupakan bilangan asli lebih besar dari 1, serta a × b × c = 180, maka banyak himpunan A yang mungkin adalah…..

A. 6
B. 8
C. 10
D. 12

Kunci jawaban: B

37. Diketahui fungsi kuadrat f(x)=ax² + bx + c dengan a>0 dan f(0)=4. Tentukan semua kemungkinan nilai a, b dan c agar 0 ≤ f(x) ≤ 4 untuk 0 ≤ x ≤ 3.

A. a = 1, b = -2 , c = 4
B. a = 4/9 , b = - 8/3 , c =4
C. a = 2/3 , b = -2, c = 4
D. a = 1/3 , b = -1, c =4

Kunci jawaban: B

38. Misalkan n menyatakan banyak perubahan posisi berurutan dari laku-laki ke perempuan atau sebaiknya dalam satu antrian. Urutan sesame laki-laki atau sesama perempuan tidak di bedakan. Contohnya, dalam antrian yang terdiri dari 4 laki laki (L) dan 6 perempuan (P) dengan ...

A. 1
B. 3
C. 5
D. 7

Kunci jawaban: C

39. Jika ab + ab + ab = cbb dan setiap huruf yang berbeda menyatakan angka yang berdeda juga, maka nilai a, b, dan c adalah ....

A. a=2,b=3,c=7a=2, b=3, c=7a=2,b=3,c=7
B. a=3,b=2,c=7a=3, b=2, c=7a=3,b=2,c=7
C. a=4,b=1,c=9a=4, b=1, c=9a=4,b=1,c=9
D. a=5,b=2,c=8a=5, b=2, c=8a=5,b=2,c=8

Kunci jawaban: B

40. Banyak cara mendapatkan empat bilangan asli ganjil (dengan urutan tidak diperhatikan) yang berjumlah 22 adalah ....

A. 6
B. 8
C. 10
D. 12

Kunci jawaban: C

41. Diketahui banyak suku suatu barisan aritmetika adalah genap. Jumlah suku-suku dengan nomor ganjil adalah 32 dan jumlah suku-suku dengan nomor genap adalah 50. Jika selisih suku terakhir dan suku pertamanya adalah 34, maka banyak suku pada barisan tersebut adalah ....

A. 6
B. 8
C. 10
D. 12

Kunci Jawaban: B

42. Dito mencatat bahwa semester ini dia telah mengikuti delapan ulangan harian pelajaran Matematika. Nilai ulangan diberikan pada skala 100. Catatan Dito menunjukkan bahwa rata-rata nilai setelah ulangan ke-7 naik 2 poin dibandingkan rata-rata nilai sampai ulangan ke-6. Sedangkan rata-rata nilai sampai ulangan ke-8 juga naik 2 poin dibanding rata-rata nilai sampai ulangan ke-7. Selisih nilai ulangan ke-8 dan ke-7 adalah ... poin.

A. 6
B. 8
C. 10
D. 12

Kunci Jawaban: C

43. Pak Tani memiliki 500 ekor ayam yang terdiri dari ayam pedaging dan ayam petelur. Sebagian ayam berwarna merah dan sebagian lagi berwarna putih. Banyak ayam petelur dan berwarna merah adalah 100 ekor. Jika diambil satu ekor ayam secara acak, maka peluang untuk mendapatkan ayam pedaging adalah sama dengan peluang untuk mendapatkan ayam berwarna putih, yaitu sebesar 3/5. Banyak ayam pedaging yang berwarna merah adalah ... .

A. 50
B. 75
C. 100
D. 125

Kunci Jawaban: B

44. Rani dan Susi masing-masing memilih empat angka berbeda yang merupakan anggota dari {1, 2, 3, 6, 8, 9} untuk menyusun dua buah bilangan dua angka. Jika mereka masing­masing menjumlahkan kedua bilangan yang disusun, maka hasilnya adalah bilangan tiga angka. Notasikan jumlah bilangan yang diperoleh Rani dan Susi berturut-turut adalah r dan s. Diketahui bahwa r bersisa 2 jika dibagi 47. Jika s memiliki nilai terbesar yang mungkin, maka r + s = ... .

A. 278
B. 325
C. 372
D. 419

Kunci Jawaban: C

45. Diketahui ABCD adalah segiempat talibusur pada lingkaran yang memiliki jari-jari luar 5 cm. Diketahui AD diameter lingkaran, panjang AB = 5 cm, dan panjang AC = 6 cm. Keliling ABCD adalah ... cm.

A. 24
B. 26
C. 28
D. 30

Kunci Jawaban: C

46. Jika kurva parabola y = x² + 4x - 5 dicerminkan terhadap garis y = x, kemudian digeser ke arah sumbu-X positip sejauh 2 satuan, maka diperoleh kurva dengan persamaan ...

A. y=x2−4x+1y = x² - 4x + 1y=x2−4x+1
B. y=x2−4x−1y = x² - 4x - 1y=x2−4x−1
C. y=x2−4x−3y = x² - 4x - 3y=x2−4x−3
D. y=x2−4x+3y = x² - 4x + 3y=x2−4x+3

Kunci Jawaban: B

47. Jumlah 1007 buah bilangan bulat positif berbeda adalah 1023076. Tidak ada satupun dari bilangan-bilangan tersebut yang lebih besar dari 2014. Minimal banyaknya bilangan ganjil pada deret bilangan tersebut adalah ....

A. 14
B. 15
C. 16
D. 17

Kunci Jawaban: C

48. Pada sebuah permainan disediakan sejumlah kartu bernomor semua bilangan prima berbeda yang bernilai kurang dari 100 dalam suatu wadah tertutup. Permainan dilakukan dengan mengambil 2 kartu secara acak dan memeriksa bilangan yang tertera pada kartu, apakah jumlahnya merupakan bilangan prima atau bukan. Jika jumlahnya bukan bilangan prima, ia diberi kesempatan mencoba kembali sampai total 3 kali pengambilan. Seorang pemain akan memenangkan permainan, jika ia berhasil mendapatkan jumlah prima pada maksimal pengambilan ke tiga. Berapa peluang seorang pemain memenagkan permainan tersebut?

A. 716/167​
B. 916/169​
C. 1116/1611​
D. 1316/1613​

Kunci Jawaban: C

49. Diketahui x dan y adalah bilangan bulat positif. Salah satu solusi dari 20x + 14y = 2014 adalah (x,y) = (100, 1). Satu solusi yang lain adalah ....

A. (93, 14)
B. (86, 27)
C. (79, 40)
D. (72, 53)

Kunci Jawaban: A

50. Terdapat bilangan ribuan dengan jumlah angka-angkanya 8. Contoh bilangan ini adalah 1232. Bilangan yang memenuhi sifat ini ada sebanyak ....

A. 21
B. 24
C. 27
D. 30

Kunci Jawaban: B

51. Diketahui dua buah himpunan A dan B dengan
A = {(x, y)|1987 ≤ y < x>B = {(x, y)|y ≤ 2013 – x dengan x dan y bilangan bulat} Banyak anggota himpunan A – B adalah ...

A. 325
B. 338
C. 351
D. 364

Kunci Jawaban: C

52. Diberikan bujursangkar dengan panjang sisi sama dengan 2√3. Didalam bujursangkar tersebut terdapat dua segitiga sama sisi dengan alas merupakansisi-sisi bujursangkar yang berhadapan. Perpotongan kedua segitiga sama sisi membentuk rhombus. Luas rhombus sama dengan ...

A. 6√3
B. 9√3
C. 12√3
D. 18√3

Kunci Jawaban: B

53. Sebuah silinder memiliki tinggi 5 cm dan volume 20 cm3. Luas permukaan bola terbesar yang mungkin diletakkan ke dalam silinder tersebut adalah .. ..

A. 16π
B. 20π
C. 25π
D. 36π

Kunci Jawaban: C

54. Jumlah tiga bilangan adalah 19. Jika bilangan pertama dan bilangan kedua masing-masing dikurangi 1, maka diperoleh dua bilangan dengan rasio 1 : 3. Jika bilangan kedua dan ketiga masing-masing ditambah 3, maka diperoleh dua bilangan dengan rasio 5 : 6. Selisih bilangan terbesar dan terkecil adalah .. ..

A. 5
B. 7
C. 9
D. 11

Kunci Jawaban: C

55. Lima belas bilangan prima pertama dituliskan berturut-turut pada lima belas kartu. Jika semua kartu tersebut diletakkan dalam sebuah kotak dan kemudian diambil secara acak dua buah kartu berturut-turut tanpa pengembalian, maka peluang terambil dua kartu dengan jumlah dua bilangan tertulis merupakan bilangan prima adalah ...

A. 28/105
B. 32/105
C. 36/105
D. 40/105

Kunci Jawaban: B

56. Rata-rata nilai dari 25 siswa adalah 40. Jika selisih rata-rata nilai 5 siswa terendah dan 20 siswa sisanya adalah 25, maka nilai rata-rata 5 siswa terendah adalah ...

A. 15
B. 20
C. 25
D. 30

Kunci Jawaban: B

57. Dalam sebuah kotak terdapat beberapa bola dengan empat macam warna yakni : biru, merah, kuning dan putih. Paling sedikit terdapat 10 bola untuk masing-masing warna. Bola diambil satu demi satu dari dalam kotak tersebut secara acak tanpa pengembalian. Banyak pengambilan yang harus dilakukan untuk memastikan mendapatkan 6 bola dengan warna sama adalah ...

A. 21
B. 22
C. 23
D. 24

Kunci Jawaban: D

58. Diketahui segitiga sama sisi dengan panjang sisi 10 cm . Jika dibuat lingkaran yang berpusat di titik tengah salah satu sisi segitiga dengan jari-jari 5 cm, maka luas daerah di dalam lingkaran dan di luar segitiga adalah..... cm.

A. 25π - 25√3
B. 25π - 20√3
C. 25π - 15√3
D. 25π - 10√3

Kunci Jawaban: A

59. Tim Sepakbola terdiri atas 25 orang, masing-masing diberi kaos bernomor 1 sampai dengan 25. Banyak cara memilih tiga pemain secara acak dengan syarat jumlah nomor kaos mereka habis dibagi tiga adalah ...

A. 450
B. 500
C. 575
D. 625

Kunci Jawaban: C

60. Indah dan Nian bermain lempar dadu secara bergantian dimulai dengan lemparan pertama giliran Indah. Seseorang akan memenangkan permainan jika ia mendapatkan mata dadu 1 tetapi  lawannya tidak mendapatkan mata dadu 2 atau 3 pada lemparan sebelumnya. Peluang Indah pada giliran yang ketiga melempar (lemparan kelima) akan menang adalah ....

A. 5/216
B. 7/216
C. 11/216
D. 13/216

Kunci Jawaban: B

*) Disclaimer: Soal di atas hanya digunakan sebagai bahan latihan dan bukan soal sebenarnya.

(Tribunnews.com/Yunita Rahmayanti)