TRIBUN-BALI.COM, DENPASAR – Simak nih, inilah jawaban soal Matematika kelas 9 Semester 1 Halaman 34 35 36 Kurikulum Merdeka, Uji Kompetensi Bab 1 tentang soal 11 sampai 20.

Kali ini kita akan membahas soal bab ke 1 yang berjudul Sistem Persamaan Linear Dua Variabel pada halaman 34 35 36, kegiatan siswa Uji Kompetensi Bab I tentang soal nomor 11 sampai 20.

Siswa diharapkan untuk mengerjakan soal yang ada di buku Matematika kelas 9 Semester 1 halaman 34 35 36 Kurikulum Merdeka secara mandiri.

Kunci jawaban Matematika kelas 9 halaman 34 35 36 Kurikulum Merdeka hanya untuk orang tua atau wali dalam membimbing siswa menjawab pertanyaan.

Berikut jawaban dan pembahasan soal Matematika kelas 9 halaman 34 35 36 Kurikulum Merdeka sesuai dengan buku siswa Matematika edisi tahun 2022.

Uji Kompetensi Bab I

Soal nomor 11 - 20

11. PERDAGANGAN.

Harga 5 kg jeruk dan 2 kg apel adalah Rp125.000,00. Sedangkan harga 3 kg jeruk dan 4 kg apel Rp131.000,00.

Tentukan uang yang harus dibayarkan apabila membeli 7 kg jeruk dan 1 kg apel.

12. GEOMETRI.

Diketahui dua sudut saling berpenyiku. Besar sudut yang lebih besar adalah 6° lebih dari empat kali ukuran sudut yang lebih kecil.

Tentukan besar kedua sudut tersebut.

13. KECEPATAN.

Alex dan Dava adalah atlet balap sepeda, mereka sedang melakukan balapan dengan jarak rute balap sejauh 2 km.

Kedua pembalap mulai pada waktu yang sama dan melaju dengan kecepatan konstan. Berikut tabel yang memberikan informasi tentang waktu dan jarak tempuh Dava mengendarai sepeda:

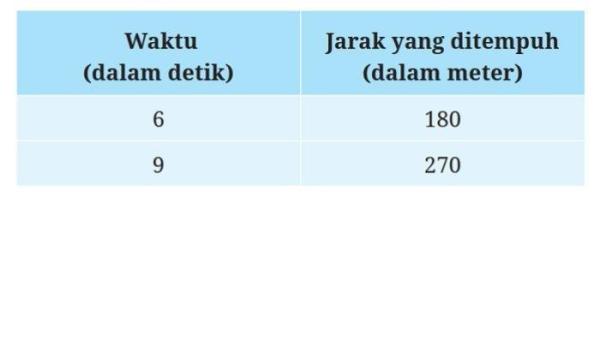
Alex menempuh seluruh balapan dengan kecepatan tetap 30 meter per detik. Apakah ada pemenang dari balapan tersebut?

14. PINJAMAN.

Seorang pedagang meminjam uang untuk modal usahanya. Ia mengambil dua pinjaman dengan total Rp8.000.000,00.

Pinjaman pertama dengan bunga sebesar 5 persen per tahun dan pinjaman kedua dengan bunga tahunan sebesar 3%.

Bunga tahun pertama adalah Rp310.000,00. Berapa besar pinjaman masingmasing?

15. KECEPATAN.

Sebuah motor menempuh jarak 240 km dalam waktu yang sama dengan sebuah mobil yang menempuh jarak 222 km.

Jika laju motor adalah 6 km/jam lebih cepat dari laju mobil, tentukan kecepatan mobil dan motor tersebut.

16. GERAK DENGAN ARUS.

Sebuah bola pingpong dilempar dari ketapel (lihat Gambar 1.22).

Ketika berlawanan dengan angin kecepatannya adalah 6 m/s sedangkan ketika searah dengan angin kecepatannya 10 m/s.

Tentukan kecepatan angin dan kecepatan bola pingpong.

17. NUTRISI.

Seorang apoteker memiliki dua bubuk suplemen vitamin. Bubuk pertama mengandung 20% vitamin B1 dan 10% vitamin B2.

Bubuk kedua mengandung 15% vitamin B1 dan 20% vitamin B2.

Berapa miligram masing-masing bubuk yang harus digunakan apoteker untuk membuat campuran yang mengandung 130 mg vitamin B1 dan 80 mg vitamin B2?

18. MASALAH INVESTASI.

Allegra memiliki uang Rp84.000.000,00 untuk diinvestasikan. Ia membagi uangnya untuk diinvestasikan pada dua rekening yang berbeda.

Hasil investasi tahunan rekeningnya adalah 4?n 6%. Pada akhir tahun Allegra memperoleh hasil investasi Rp4.560.000,00. Tentukan besar uang yang diinvestasikan pada setiap rekening.

19. GEOMETRI.

Tentukan sudut x dan y pada gambar berikut.

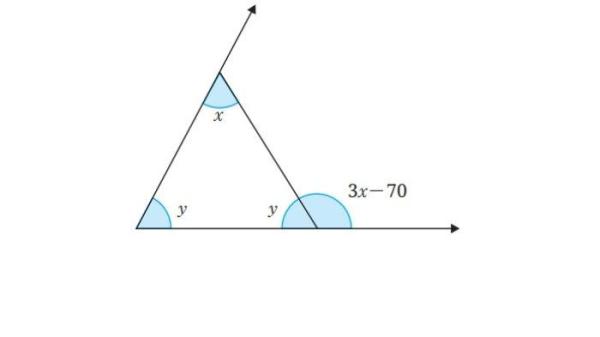
20. LARUTAN. Seorang pengrajin perhiasan akan mencampurkan logam dengan kandungan paladium 48?n logam dengan kandungan paladium 84% untuk mendapatkan 32 gram logam baru dengan kandungan palladium 75%.

Berapa gram berat dari masing masing logam yang harus digunakan?

Jawaban:

Soal nomor 11

Misalkan x merupakan harga satu kilogram jeruk dan y merupakan harga satu kilogram apel, maka diperoleh sistem persamaan sebagai berikut.

5x + 2y = 125.000 persamaan I

3x + 4y = 131.000 persamaan II

Untuk mengeliminasi variabel y, persamaan I dikalikan dengan 2 dan persamaan II dikalikan dengan 1.

Jadi uang yang harus dibayarkan apabila membeli 7 kg jeruk dan 1 kg apel adalah Rp139.000,00.

Soal nomor 12

Misalkan x dan y merupakan dua sudut yang saling berpenyiku, dengan x merupakan sudut yang lebih besar. Diperoleh sistem persamaan sebagai berikut.

x + y = 90 persamaan I

x = 6 + 4y persamaan II

Substitusikan persamaan II ke persamaan I, diperoleh:

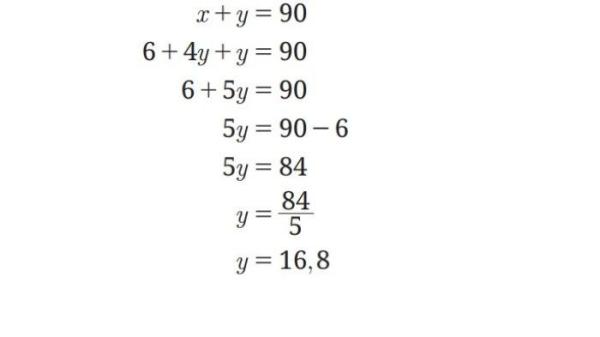
Substitusikan nilai y = 16,8 ke x + y = 90 diperoleh nilai x = 73,2. Jadi besar kedua sudut tersebut adalah 16,8° dan 73,2°.

Soal nomor 13

Misalkan x merupakan waktu balapan sepeda (dalam detik) dan y merupakan jarak yang ditempuh (dalam meter).

Kasus Dava

Diketahui dua titik (6,180) dan (9,270)

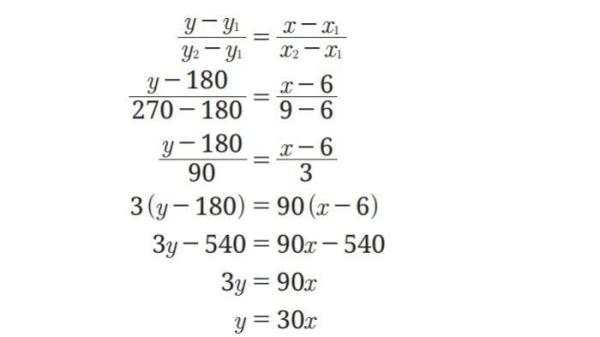
Kasus Alex

Diketahui kecepatan 30 meter per detik. Ingat rumus kecepatan adalah jarak dibagi waktu sehingga diperoleh persamaan y = 30x.

Pada permasalahan ini diperoleh sistem persamaan

y = 30x persamaan kasus Dava

y = 30x persamaan kasus Alex

Jika di gambar grafik kedua garis berimpit, artinya perlombaan seri.

Soal nomor 14

Misalkan x merupakan banyak pinjaman pertama dan y merupakan banyak pinjaman kedua, maka diperoleh sistem persamaan sebagai berikut.

x + y = 8.000.000 persamaan I

0,5x + 0,03y = 310.000 persamaan II

Persamaan I diubah bentuk menjadi x =8.000.000 - y

Substitusikan x = 8.000.000 ke persamaan II, diperoleh:

Substitusikan nilai y = 4.500.000 ke x = 8.000 000 diperoleh

nilai x = 3.500.000.

Jadi banyak pinjaman pertama adalah Rp3.500.000,00 dan pinjaman kedua Rp4.000.000,00.

Soal nomor 15

Misalkan p dan q berturut-turut menyatakan kecepatan motor dan mobil. Ingat rumus kecepatan = jarak/waktu

Diperoleh sistem persamaan sebagai berikut.

240/p = 222/q persamaan I

p = q + 6 persamaan II

Substitusikan persamaan II ke persamaan I, diperoleh:

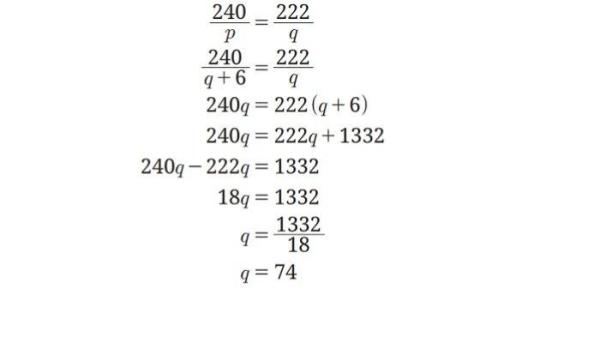
Substitusikan nilai q = 74 ke persamaan II diperoleh nilai p = 80.

Jadi kecepatan motor dan mobil berturut-turut adalah 80 km/jam dan 74 km/jam.

Soal nomor 16

Misalkan x merupakan kecepatan bola dan y merupakan kecepatan angin, maka diperoleh sistem persamaan sebagai berikut.

x - y = 6 persamaan I

x + y = 10 persamaan II

Persamaan I diubah bentuk menjadi x = 6 + y.

Substitusikan x = 6 + y ke persamaan II, diperoleh:

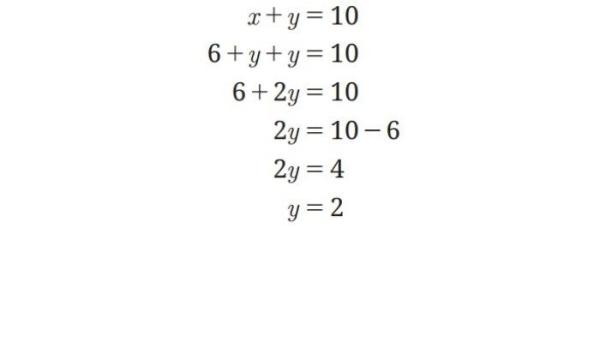
Substitusikan nilai y = 2 ke x = 6 + y diperoleh nilai x = 8.

Jadi kecepatan bola adalah 8 m/s dan kecepatan angin adalah 2 m/s.

Soal nomor 17

Misalkan x merupakan banyak bubuk pertama (dalam miligram) dan y merupakan banyak bubuk kedua (dalam miligram), maka diperoleh sistem persamaan sebagai berikut.

0,2x + 0,15y = 130 persamaan I

0,1x + 0,2y = 80 persamaan II

Untuk mengeliminasi variabel x, persamaan I dikalikan dengan 1 dan persamaan II dikalikan dengan 2.

Jadi banyak bubuk pertama adalah 560 mg dan banyak bubuk kedua 120 mg.

Soal nomor 18

Misalkan x merupakan besar uang yang diinvestasikan pada rekening pertama dan y merupakan besar uang yang diinvestasikan pada rekening kedua, maka diperoleh sistem persamaan sebagai berikut.

x + y = 84.000.000 persamaan I

0,0x + 0,06y = 4.500.000 persamaan II

Persamaan I diubah bentuk menjadi x y = - 84. . 000 000.

Substitusikan x y = - 84. . 000 000 ke persamaan II, diperoleh:

Substitusikan nilai y = 60.000.000 ke x = 84.000.000 - y diperoleh nilai x = 24.000.000.

Jadi besar uang pada tiap rekening adalah Rp24.000.000,00 dan Rp60.000.000,00.

Soal nomor 19

x + 2y = 180

3x - 70 + y = 180

=

x + 2y = 180 persamaan I

3x + y = 250 persamaan II

Persamaan I diubah bentuk menjadi x = 180 - 2y.

Substitusikan x = 180 - 2y ke persamaan II, diperoleh:

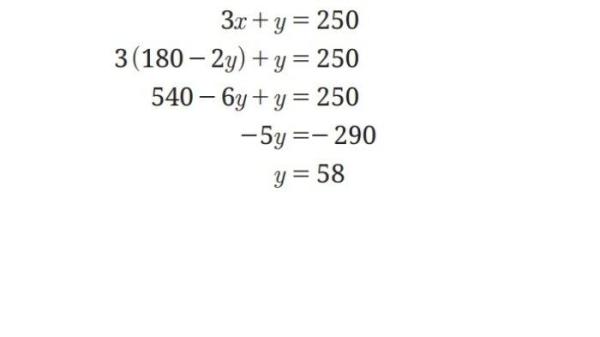
Substitusikan nilai y = 58 ke x = 180 - 2y diperoleh nilai x = 64.

Jadi, sudut y = 58° dan sudut x = 64°.

Soal nomor 20

Misalkan x merupakan berat logam pertama dan y merupakan berat logam kedua, maka diperoleh sistem persamaan sebagai berikut.

x + y = 32

0,48x + 0,84y = 0,75 (32)

=

x + y = 32 persamaan I

0,48x + 0,84y = 24 persamaan II

Persamaan I diubah bentuk menjadi x = 32 - y.

Substitusikan x = 32 - y ke persamaan II, diperoleh:

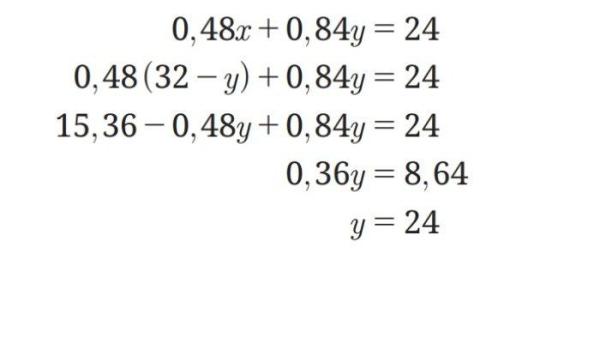
Substitusikan nilai y = 24 ke x = 32 - y diperoleh nilai x = 8.

Jadi berat dari masing-masing logam asli yang harus digunakan adalah 8 gram dan 24 gram.

Keterangan: (") berarti pangkat

Demikian jawaban soal Matematika kelas 9 Semester 1 halaman 34 35 36 Kurikulum Merdeka, kegiatan siswa Uji Kompetensi Bab I sesuai dengan buku siswa Matematika edisi tahun 2022.

Disclaimer

Kunci jawaban diatas bersifat alternatif jawaban sehingga para siswa bisa memberikan eksplorasi jawaban lain.

Kunci jawaban soal diatas bisa saja berbeda sesuai dengan pemahaman tenaga pengajar atau murid. (*)